Nadaraya-Watsonを理解したい

データサイエンス教師あり学習
更新日：2022-02-22

はじめに

1964 年に Nadaraya と Watson によって考案された Nadaraya-Watson は現在でも使われている手法です。カーネル平滑化の 1 つの手法であり、回帰手法の 1 つでもあり、局所線形回帰の兄弟のような関係を持っています。

本記事では、そんな Nadaraya-Watson を理解したいをコンセプトに書きました。

問題設定

Nadaraya-Watson について語る前に問題設定を書いておきます。

データセット $(\mathbf{x}_i,\mathbf{y}_i)_{i=1}^{n}(i=0,1,2,\dots,n)$ が与えられているとします。 $x$ は入力で、 $y$ は出力です。

また、 $x^{\ast}$ を新規の入力データとして、それに対応する出力を $y^{\ast}$ とします。

このときに、データセットを学習して $\mathbf{y^{\ast}} \simeq f(\mathbf{x^{\ast}})$ となるような滑らかな非線形写像 $f$ を Nadaraya-Watson は推定します。

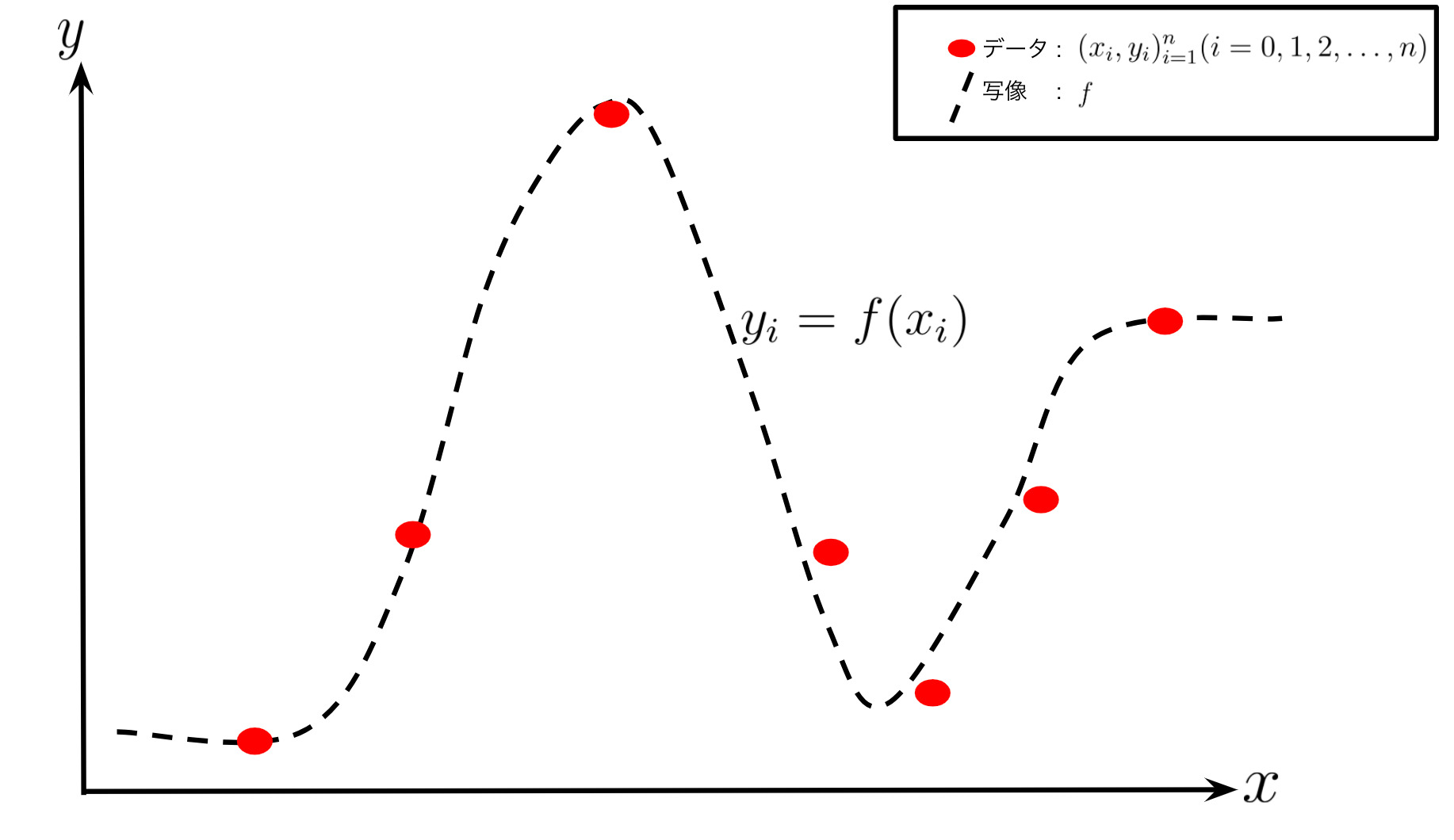
滑らかな非線形写像 $f$ を Nadaraya-Watson は推定することで、図の波線部分が推定されます。

まずはざっくりと

まず、Nadaraya-Watson についてざっくりと書きたいと思います。

Nadaraya-Watson は、局所多項式回帰における第 0 次の局所線形回帰であり、0 次元カーネル平滑化と言われます。Nadaraya-Watson では、重み付け関数であるカーネルを用いて局所的に新規のデータと学習データの距離に応じた重みを与えます。その重み平均の平均を算出することで、新規の入力 $x^{\ast}$ に対する出力 $y^{\ast}$ の推定を行います。

わかりやすく言うと、重み付き平均における重みの決定にガウス関数を使っているということです。

非線形写像 $f$ は下記の式で表されます。

f(x^{\ast})=\frac{\sum_{i=1}^N K_{\sigma}(x^{\ast},x_i)y_i}{\sum_{j=1}^N K_{\sigma}(x^{\ast},x_j)}

K_{\sigma}(x^{\ast} , x_j) = \exp(\frac{-1}{2{\sigma}^2}||x^{\ast}- x_j||^2)

$K_{\sigma}(x^{\ast} , x_j)$ は任意のカーネル関数であり、上記の式の場合はガウシアンカーネルです。新規のデータ $x^{\ast}$ と学習データ $x_i$ , $x_j$ との距離に応じて重みを決定します。

Nadaraya-Watson は局所多項式回帰における第０次の局所線形回帰ですが、1 次になると局所線形回帰と言われます。第１次の局所線形回帰について詳しくはこちらに詳しく説明されています。

Nadaraya-Watson の位置付け

Nadaraya-Watson 推定はカーネル回帰でもあり、カーネル平滑化の 1 つの手法でもあり、カーネル密度推定とも関係しています。

Nadaraya-Watson 推定のカーネル回帰やカーネル平滑化、カーネル密度推定における位置付けを明確にしておきます。

カーネル回帰とは

カーネル回帰は、確率変数の条件付き期待値を推定するためのノンパラメトリック手法です。目的は確率変数 $X$ と $Y$ の非線形関係を見つけることになります。

ノンパラメトリック回帰では、変数 $X$ に対する変数 $Y$ の条件付き期待値は次のように記述できます。

E(Y|X)=f(X)

なぜこうなるのか？

サイコロの例で考える。

形の異なる二つのサイコロを投げて大きいほうのサイコロの目を $X$ 、小さいほうのサイコロの目を $Y$ とする。条件付き期待値を計算したい確率変数を 2 つのサイコロの目の積 $XY$ とし、 $Y=3$ という情報が分かっているとする。このとき、ありうる可能性は $(X,Y)=(1,3),(2,3),(3,3),(4,3),(5,3),(6,3)$ の 6 通りであり、それぞれ確率 16 であるので

E[XY|Y=3]=1 \cdot 3 \cdot \frac{1}{6} + \cdots + 6 \cdot 3 \cdot \frac{1}{6} = \frac{21}{2}

となる。同様に $Y=y$ がわかっていると

E[XY|Y=y]=\frac{21y}{6}

というのが分かる、これは

E[XY|Y=y]={\frac{21y}{6}}

というのが分かります。これを

E[XY|Y]={\frac{21Y}{6}}

と書くと、「 $Y$ の値が決まったときの $XY$ の期待値は $\frac{21Y}{6}$ である。」と自然に読むことができる。このようなことは一般の確率変数の組 $X$ と $Y$ が与えられた場合にもいえることで、関数 $f$ をうまく見つけてきて

E[X|Y]=f(Y)

とすることができる。

この形から回帰手法として、Nadaraya-Watson 推定の式があるのです。

カーネル平滑化

カーネル平滑化は、近傍な観測データに対して局所的に重み付けをして単純なモデルをあてはめて実数値関数を推定するための統計手法です。

目的は、実数値関数を推定することからわかるように観測データを使って観測データの重要パターンや傾向を発見したり、予測をすることになります。

カーネル平滑化において、単純なモデルに直線(1 次)を当てはめるカーネル平滑化を 1 次のカーネル平滑化として局所線形回帰といいます。曲線(2 次)を当てはめれば 2 次のカーネル平滑化です。そして、N 次のカーネル平滑化は局所多項式回帰と呼ばれます。

Nadaraya-Watson 推定は、直線や曲線を当てはめずに単に観測データに対して局所的に平均をとるので 0 次のカーネル平滑化と言われています。

Nadaraya-Watson や局所線形回帰では、推定すべき回帰関数の曲率が大きいところでは比較的大きなバイアスが生じるデメリットがあります。分散の方を気にせずに、バイアスを縮小するなら局所多項式回帰を使います。

カーネル平滑化の目的と回帰手法の目的は一致します。また、上の文で回帰というワードが出てきていますように平滑化は回帰と見なせるので、カーネル回帰とカーネル平滑化は class="st-mymarker-s"断言はできませんが class="st-mymarker-s"ほぼ同じものと考えていいと思います。

カーネル密度推定

カーネル密度推定（KDE）は、確率変数の確率密度関数を推定するためのノンパラメトリックな方法です。 $(x_i)^n_{i=1}$ を(未知の)確率密度関数 $f$ を持つ独立同分布からのデータとして、その確率密度関数を推定します。各標本データの局所的近傍から得られる結果を重ね合わせて確率分布関数全体を推定（表現）しようとする特性上，標本データ数が少ないと正しい確率密度関数を得られない特徴があります。

\widehat{f_{\sigma}}(x)=\frac{1}{n{\sigma}}K_{\sigma}(x^{\ast},x_j)

カーネル密度推定は確率密度関数の推定方法、カーネル平滑化は回帰の手法です。つまり、カーネル平滑化とカーネル密度推定は別物です。

条件付き確率密度関数は、 $f(x)\gt 0$ のときに、次のように定義できます。

E(Y|X=x)=\int yf(y|x)dy=\int y\frac{f(x,y)}{f(x)}dy

f(y|x)dy=\frac{f(x,y)}{f(x)}

ここで $f(x,y)$ は $X$ と $Y$ の同時分布で、 $f(x)$ は周辺分布です。これらは以下の式が成り立ちます。

f(x,y)=\frac{1}{n}\sum_{i=1}^nK_{\sigma}(x^{\ast},x_i)K_{\sigma}(y^{\ast},y_i)

f(x)=\frac{1}{n}\sum_{i=1}^nK_{\sigma}(x^{\ast},x_i)

したがって、これらを代入して変形していくと Nadaraya-Watson の式が導出されます。

\begin{equation*}\begin{split}E(Y|X=x)&= \int \frac{y\sum_{i=1}^{n}K_{\sigma}(x^{\ast}, x_i)K_{\sigma}(y^{\ast}, y_i)}{\sum_{j=1}^nK_{\sigma}(x^{\ast}, x_j)}dy\\&=\frac{\sum_{i=1}^{n}K_{\sigma}(x^{\ast},x_i) \int y K_{\sigma}(y^{\ast}, y_i)}{\sum_{j=1}^{n}K_{\sigma}(x^{\ast}, x_j)}dy \\ &= \frac{\sum_{i=1}^{n}K_{\sigma}(x^{\ast}, x_i)y_i}{\sum_{j=1}^{n}K_{\sigma}(x^{\ast},x_j)}\end{split}\end{equation*}

二変量の同時分布 $f(x,y)$ をカーネル密度推定で推定した時、条件付き分布 $f(y|x)$ の平均値は Nadaraya-Watson と一致します。

Nadaraya-Watson の様々な呼び方

上記で述べたように Nadaraya-Watson はカーネル平滑化やカーネル回帰、カーネル密度推定と関係を持っています。ゆえに様々な呼び方で呼ばれます。その呼び方を以下にまとめておきます。

Kernel smoother
Kernel regression
Nadaraya-Watson kernel estimator
Nadaraya-Watson estimato
Nadaraya-Watson kernel regression

何をしているのか

Nadaraya-Watson は重み付け関数であるカーネルを用いて局所的に新規のデータと学習データの距離に応じた重みを与えます。

つまり、新規のデータに近いデータに対しては誤差を重く、逆に遠いデータに対しては誤差を軽く見て推定を行います。

また、データの端点以降の写像は端点データに収束する特徴があります。

イメージ図は次のようになります。曲線が多少歪んで見えるかもしれないですが気にしないでください。

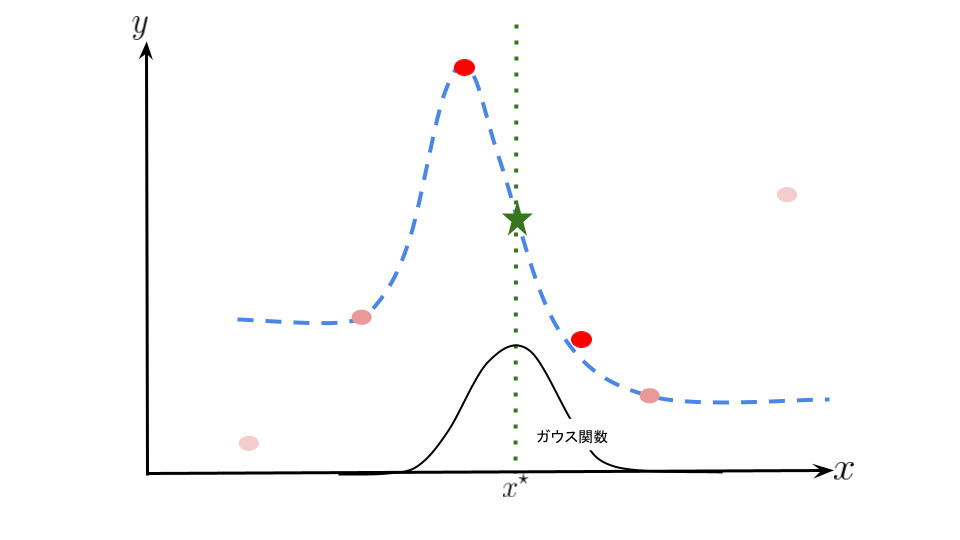
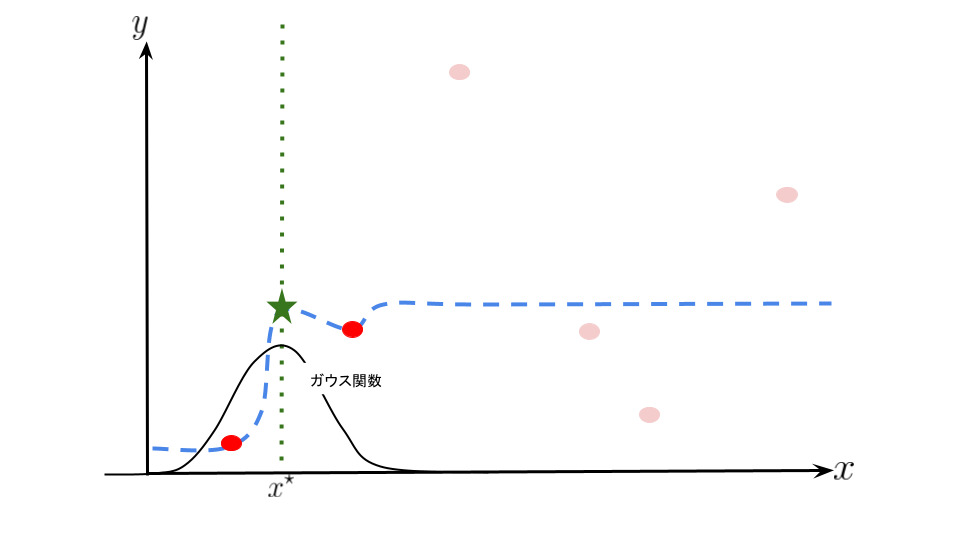
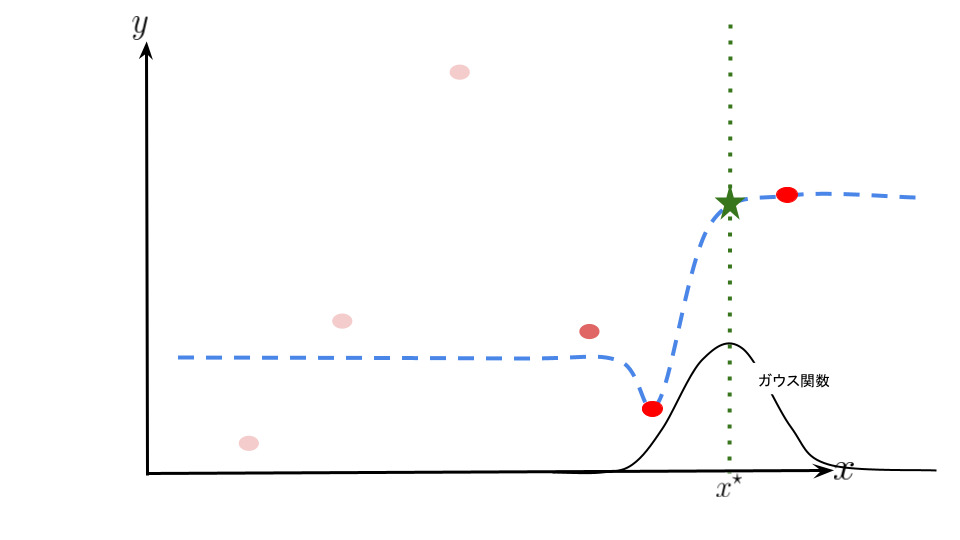
局所的に新規のデータと学習データの距離に応じた重みを与えることで写像 $f$ の推定を行っているのがなんとなくイメージできたと思います。 Nadaraya-Watson では上記の青点線の組み合わせのような感じです。

このときの誤差の重みを決める関数(カーネル関数) $K_{\sigma}(x^{\ast} , x)$ は以下の式で表されるとします。

K_{\sigma}(x^{\ast} , x_j) = \exp(\frac{-1}{2{\sigma}^2}||x^{\ast}- x_j||^2)

$\sigma$ はカーネル幅と呼ばれる（ハイパー）パラメータです。ざっくり言いますと「新規データに対する近い or 遠いを決める境目」を決めるものです．これを大きくするとより広い範囲のデータを近傍と見なします．これを究極に大きくすると全てのデータ点に対する平均値しかとりません。

実装

それでは Nadaraya-Watoton を実装して挙動を見ていきたいと思います。

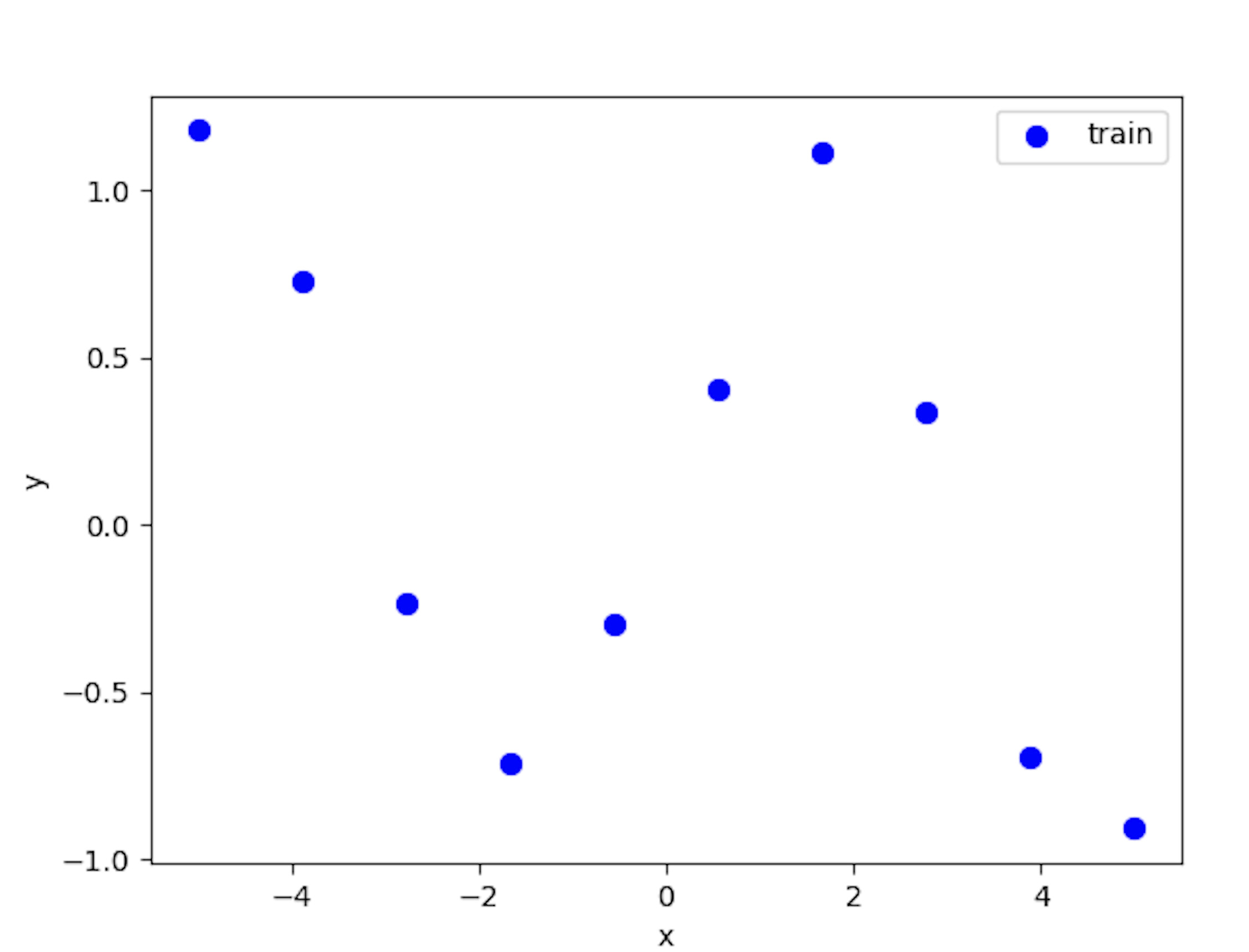
import numpy as np
import matplotlib.pyplot as plt

class NW():
  def **init**(self, sigma):
    self.sigma = sigma

  def fit(self, x, y, test_x):
    delta = test_x[:, None] - x[None, :] #新規データ - 元データ
    Dist = np.square(delta)
    kernel = np.exp((-0.5 / (self.sigma \*_ 2)) _ Dist) #ガウシアンカーネル
    k_denominator = np.sum(kernel, axis=1)
    r = kernel / k_denominator[:, None]
    pred_y = r @ y
    return pred_y

if **name** == '**main**':
  np.random.seed(0)

  train_x = np.linspace(-5, 5, 10)
  train_y = np.sin(train_x) + np.random.randn(\*train_x.shape) / 8
  test_x = np.linspace(-6, 6, 100) #新規のデータ

  nw = NW(σ:=0.8)
  pred_y = nw.fit(train_x, train_y, test_x)

  fig = plt.figure()
  plt.scatter(train_x, train_y, c='b', lw=2, label="train")
  plt.legend()
  plt.xlabel('x')
  plt.ylabel('y')
  fig.savefig("img.png")
  plt.show()

データは $y=sin(x)$ に対してガウスノイズを加えたものを使います。

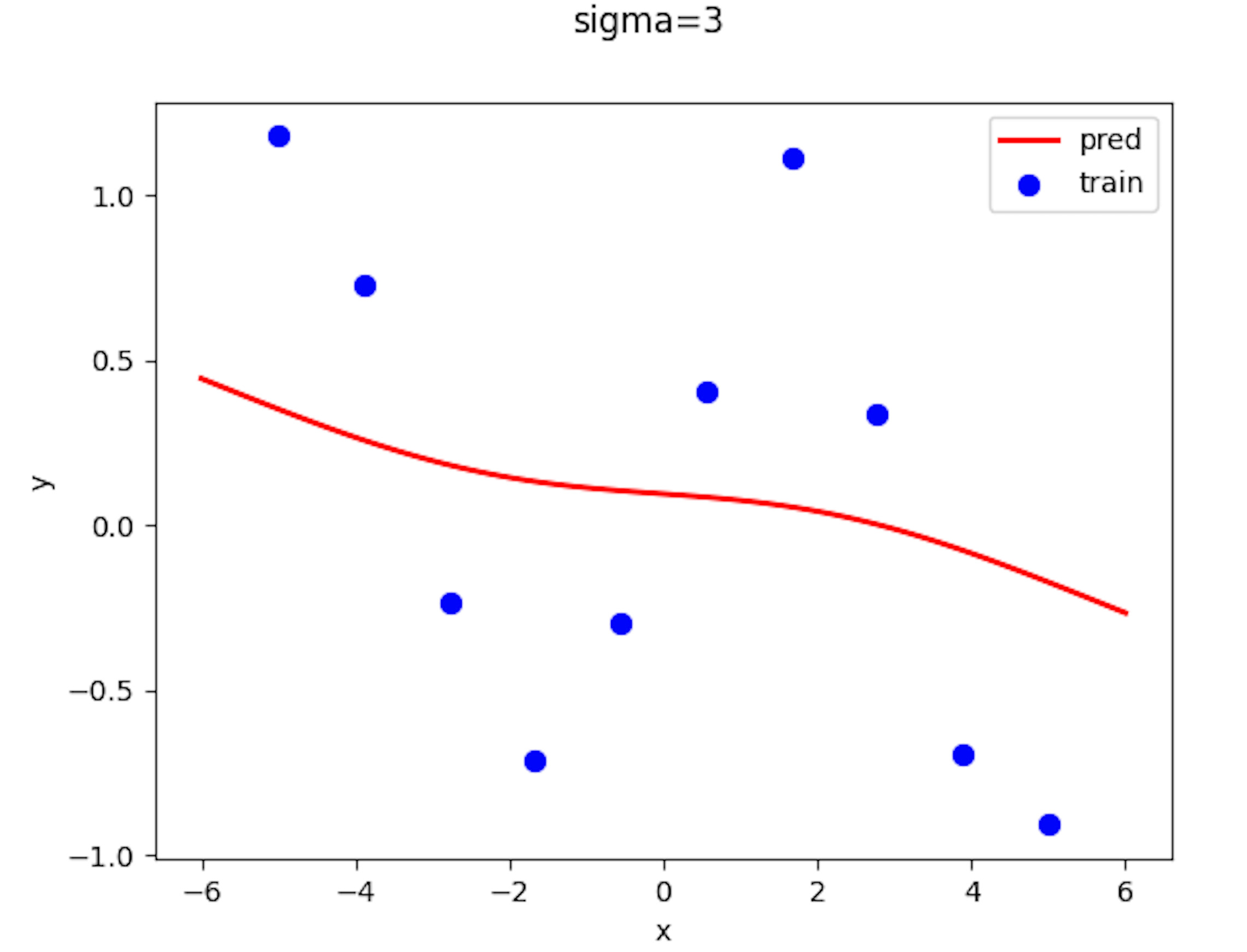
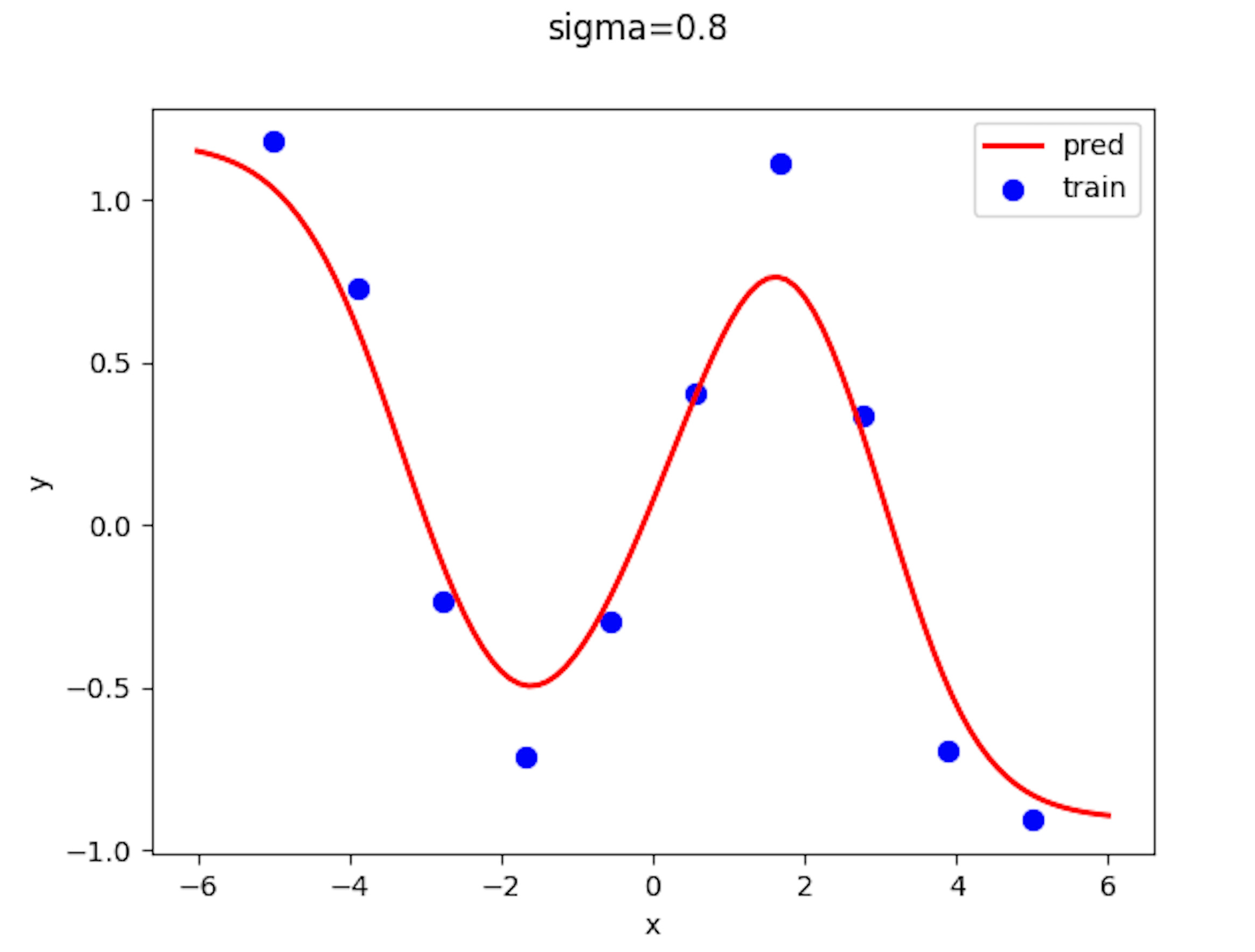
近傍半径 $\sigma=3$ 、 $\sigma=0.8$ 、 $\sigma=0.1$ でプロットした結果を貼っていきます。

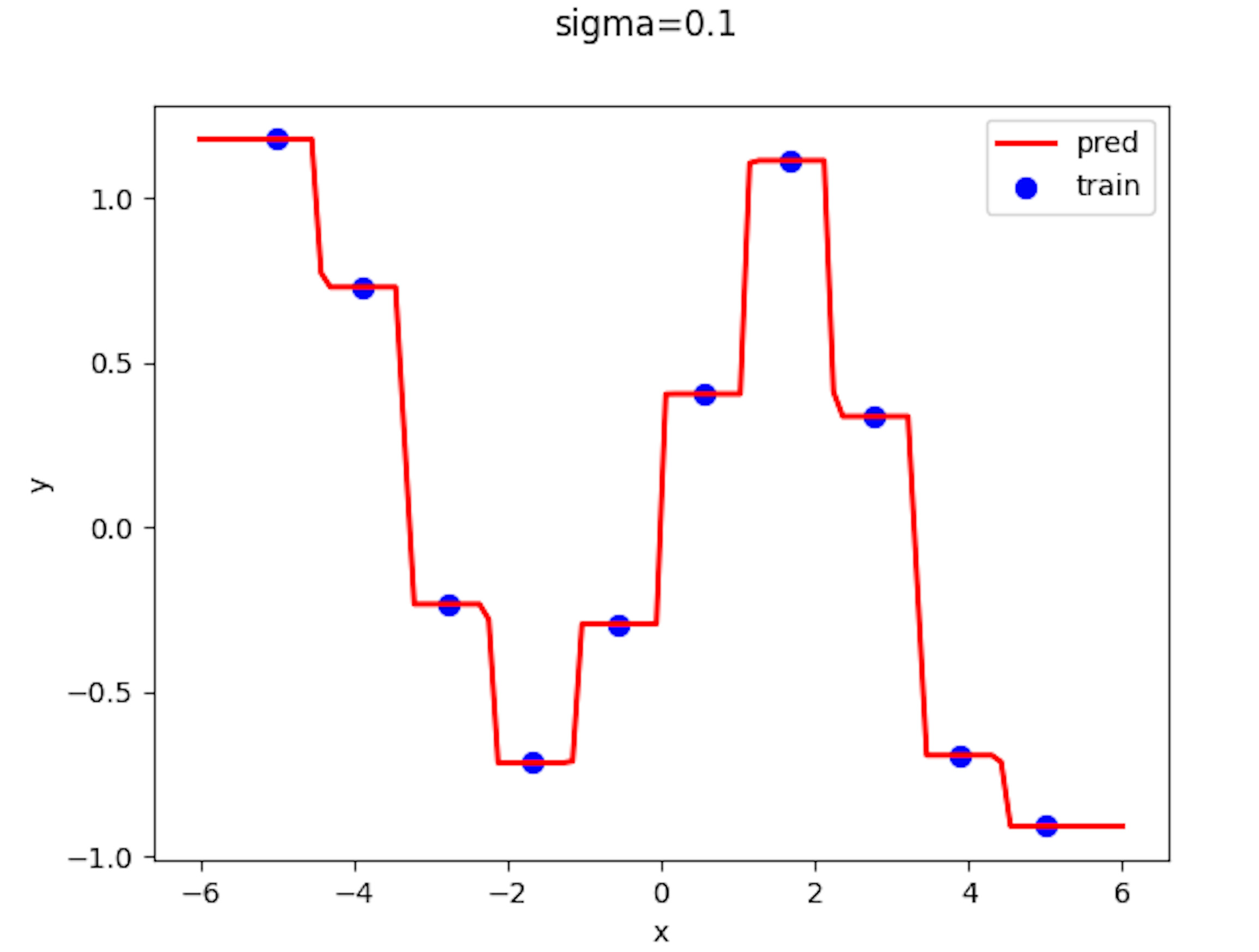
近傍半径が $0.1$ のとき推定値 $f(x)$ は入力 $x$ に最も近いデータ $x_i$ に対応する $y_i$ の値をとるようになっています。これは、Nadaraya-Watson に次のことが成り立つからです。

入力 $x$ 、出力 $y$ において $\sigma \rightarrow 0$ のとき，

f(x) \simeq y\_{i^\ast}\,, i^\ast = \underset{i}{argmin}(x - x_i)

近傍半径が小さすぎると、最も近い学習データにのみ影響を受け、その値になるのです。そのため、学習データ間の中間付近ではステップ関数のような挙動が見られるのです。これは、K 近傍法の $k$ の数 1 のときの結果と同じです。

最後に、近傍半径を小さくしていくとどうなるのかの動画を載せておきます。

最後に

ここまで読んでくださってありがとうございました。編集リクエストもお待ちしてます。

こちらもオススメです。 ↓↓↓↓↓↓↓↓↓↓↓↓