Kunst Site

固有値と固有ベクトルについて


データサイエンス数学
更新日：2022-02-22

固有値と固有ベクトルについては機械学習の理解をするには必要不可欠なので線形代数などで登場する固有値と固有ベクトルについて書いてみました。

行列とベクトルの演算

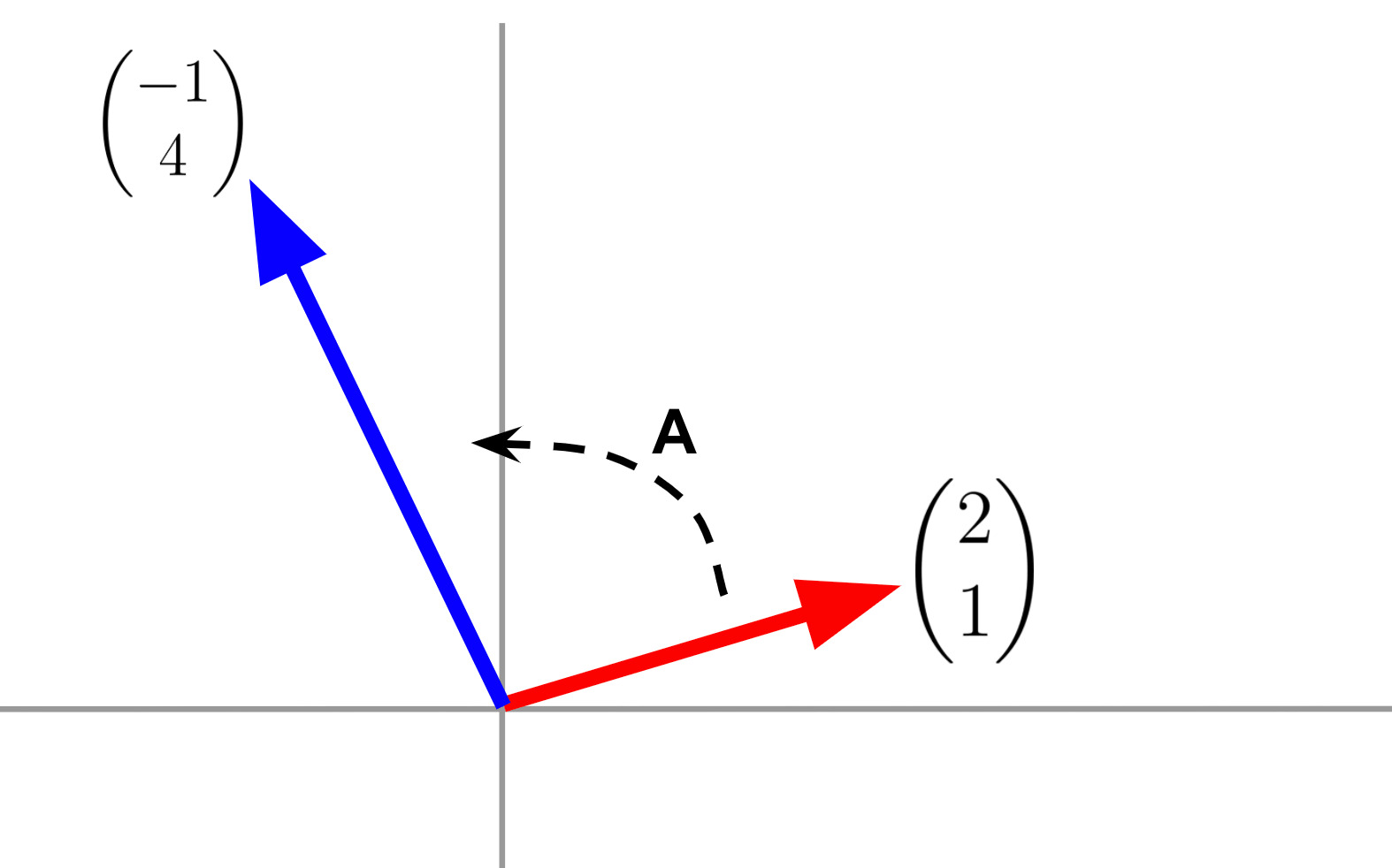
固有値と固有ベクトルの説明をする前に行列とベクトル演算についてふれておきます。 ２次元ベクトル(2,1)(2,1)が２次元空間上にあるとします。 この２次元ベクトルに対して 2 行 2 列の正方行列をかけてみます。

(2−55−6)(21)=(−14)\begin{pmatrix}2 & -5 \\ 5 & -6\end{pmatrix} \begin{pmatrix}2 \\ 1\end{pmatrix}=\begin{pmatrix} -1 & 4 \end{pmatrix}

算出された２次元ベクトルを見てみると、ベクトルの方向が変わっていることがわかります。このように、ベクトルは行列との演算によって並進や回転、拡大などの変換作用がなされます。

変換作用

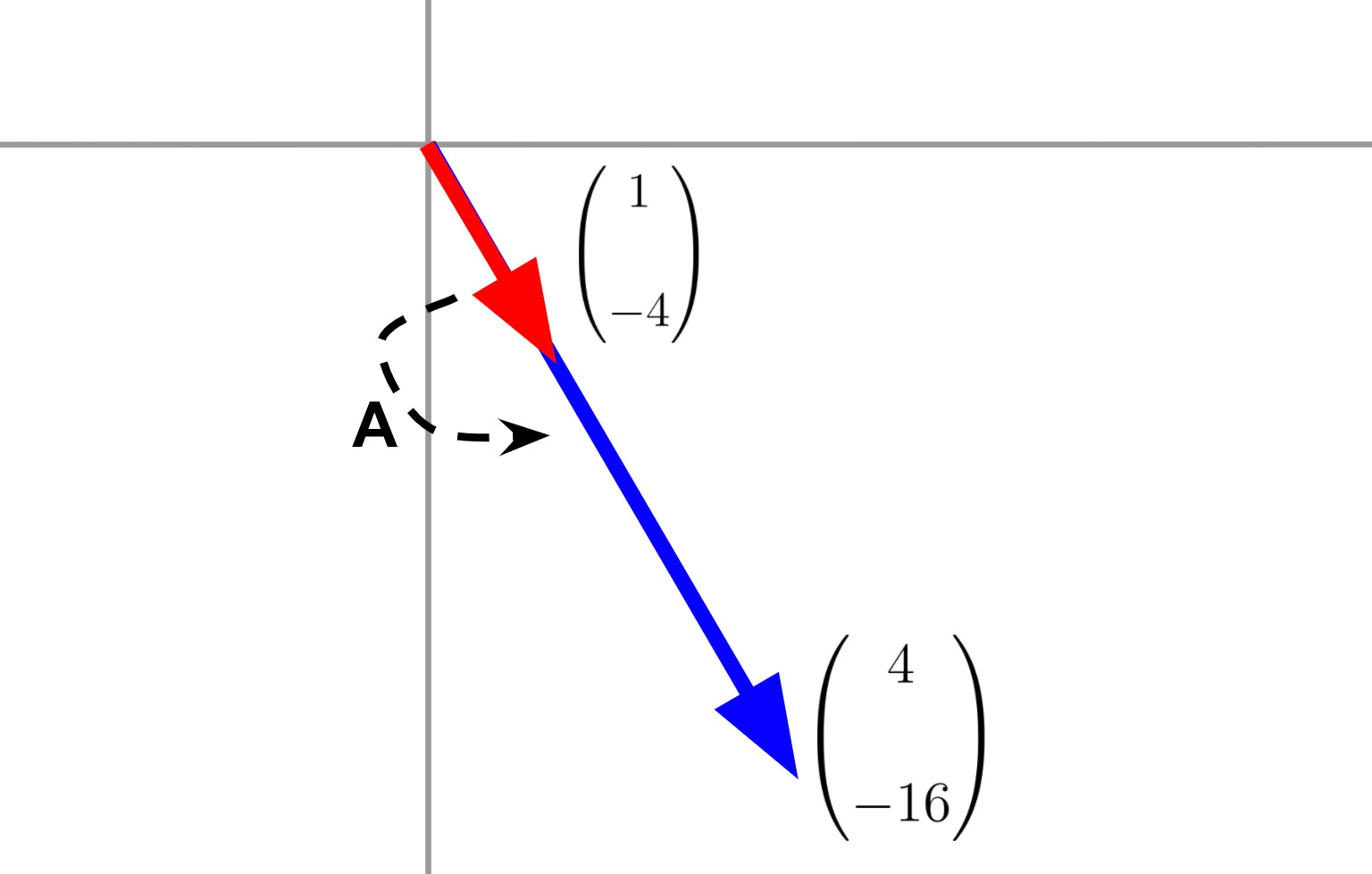
ベクトルは行列との演算によって並進や回転、拡大などの変換作用がなされるわけですが、ベクトルの方向は全く変わらず大きさだけ変化するケースも存在します。 例えば、２次元ベクトル(1,−4)(1,-4)に対して次の行列演算を行うとします。

(8145)(1−4)=(4−16)\begin{pmatrix} 8 & 1 \\ 4 & 5 \end{pmatrix} \begin{pmatrix} 1 \\ -4 \end{pmatrix}=\begin{pmatrix} 4 & -16 \end{pmatrix}

算出された２次元ベクトルは全く方向は変わっておらず大きさだけ変化しています。

変換作用2

固有値と固有ベクトル

固有値と固有ベクトルの話に戻ってきました。固有値と固有ベクトルを式で表すと次の式になります。

Ax=λxAx = \lambda x

この式の意味は、ベクトルxxに行列 A を作用されると方向は変わらずλ\lambda倍の大きさになるとうことです。先ほどの行列とベクトルの演算で話したことと同じですね。このときのxxを固有ベクトル、λ\lambdaを固有値といいます。まとめると

固有値と固有ベクトルの求め方

固有値と固有ベクトルの求め方はネットにたくさんありますが、この Qiita 記事でも行います。 次の行列 A の固有値と固有ベクトルを求めます。

A=(8145)A=\begin{pmatrix} 8 & 1 \\ 4 & 5 \end{pmatrix}

固有値、固有ベクトルの式から変形していきます。

Ax=λx⇔∣A−λI∣=0⇔∣(8145)−(λ00λ)∣=0⇔∣8−λ114−λ∣=0\begin{align} & Ax = \lambda x \\ \\ \Leftrightarrow & \big| A-\lambda I \big| = 0 \\ \\ \Leftrightarrow & \left| \begin{matrix} \left( \begin{matrix} 8 & 1 \\ 4 & 5 \end{matrix} \right) - \left( \begin{matrix} \lambda & 0 \\ \\ 0 & \lambda \end{matrix} \right) \end{matrix} \right| = 0 \\ \\ \Leftrightarrow & \left| \begin{matrix} 8-\lambda & 1 \\ 1 & 4-\lambda \\ \end{matrix} \right| = 0 \end{align}

行列式ad−bcad-bcより

;(8−λ)(5−λ)=0⇔;λ2−6λ+36=0⇔;(λ−4)(λ−9)=0\begin{align} &; (8-\lambda)(5-\lambda) = 0 \\ \\ \Leftrightarrow &; \lambda^2-6\lambda +36 = 0 \\ \\ \Leftrightarrow &; (\lambda-4)(\lambda-9)=0 \end{align}

これで固有値λ=4,9\lambda=4,9が求まりました。各々の固有値に対応する固有ベクトルを求めます。

λ=4

λ=4\lambda=4 を Ax=λxAx = \lambda xへ代入します。

;(8−4145−4)(x1x2)=(00)⇔(4141)(x1x2)=(00)\begin{align} &; \begin{pmatrix} 8-4 & 1 \\ 4 & 5-4 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} \\ \\ \Leftrightarrow & \begin{pmatrix} 4 & 1 \\ 4 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{align}

したがって、4x1+x2=04x_1+x_2=0なのでttを任意の実数として

{x1=tx2=4t\left\{ \begin{array}{ll} x_1=t & \\ x_2=4t & \end{array} \right.

となるので固有ベクトルはttを任意の実数として次の値になります。

t(14)t\begin{pmatrix} 1 \\ 4 \end{pmatrix}

λ=9

λ=9\lambda=9 を Ax=λxAx = \lambda xへ代入します。

(8−9145−9)(x1x2)=(00)⇔(−114−4)(x1x2)=(00)\begin{align} & \begin{pmatrix} 8-9 & 1 \\ 4 & 5-9 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} \\ \\ \Leftrightarrow & \begin{pmatrix} -1 & 1 \\ 4 & -4 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{align}

したがって、−x1+x2=0-x_1+x_2=0なのでttを任意の実数として

{x1=tx2=t\left\{ \begin{array}{ll} x_1=t & \\ x_2=t & \end{array} \right.

となります。したがって、固有ベクトルはttを任意の実数として次の値になります。

t(11)t\begin{pmatrix} 1 \\ 1 \end{pmatrix}

これで固有値と、それぞれの固有値に対応する固有ベクトルが求まりました。

機械学習における固有値と固有ベクトル

ここまで固有値と固有ベクトルについての基本的なことについて述べました。しかし、こういった固有値と固有ベクトルが機械学習の世界でどのように活用されているかがよくわからないと思います。

機械学習の世界では、共分散行列の固有値、固有ベクトルを求めるといった場面によく遭遇します。共分散行列について詳しくは他記事を参考にしてもらうとして、簡単に説明しますと共分散行列はデータの形を定義します。 共分散行列の固有ベクトルがわかるとデータ全体を説明する方向がわかります。つまり、大きな固有値に対応する固有ベクトルほどデータ全体を説明するのに重要というわけです。